mamba

mamba瓶颈测量

加载huggingface上的state-spaces/mamba-130m-hf模型在wikitext-2-raw-v1的test数据集上进行测量

SSM scan          341938.203
SSM parameters    155749.540
RMSNorm           137193.504
Convolution       136929.270
in_proj            80687.654
out_proj           73341.112
Name: time_ms, dtype: float64

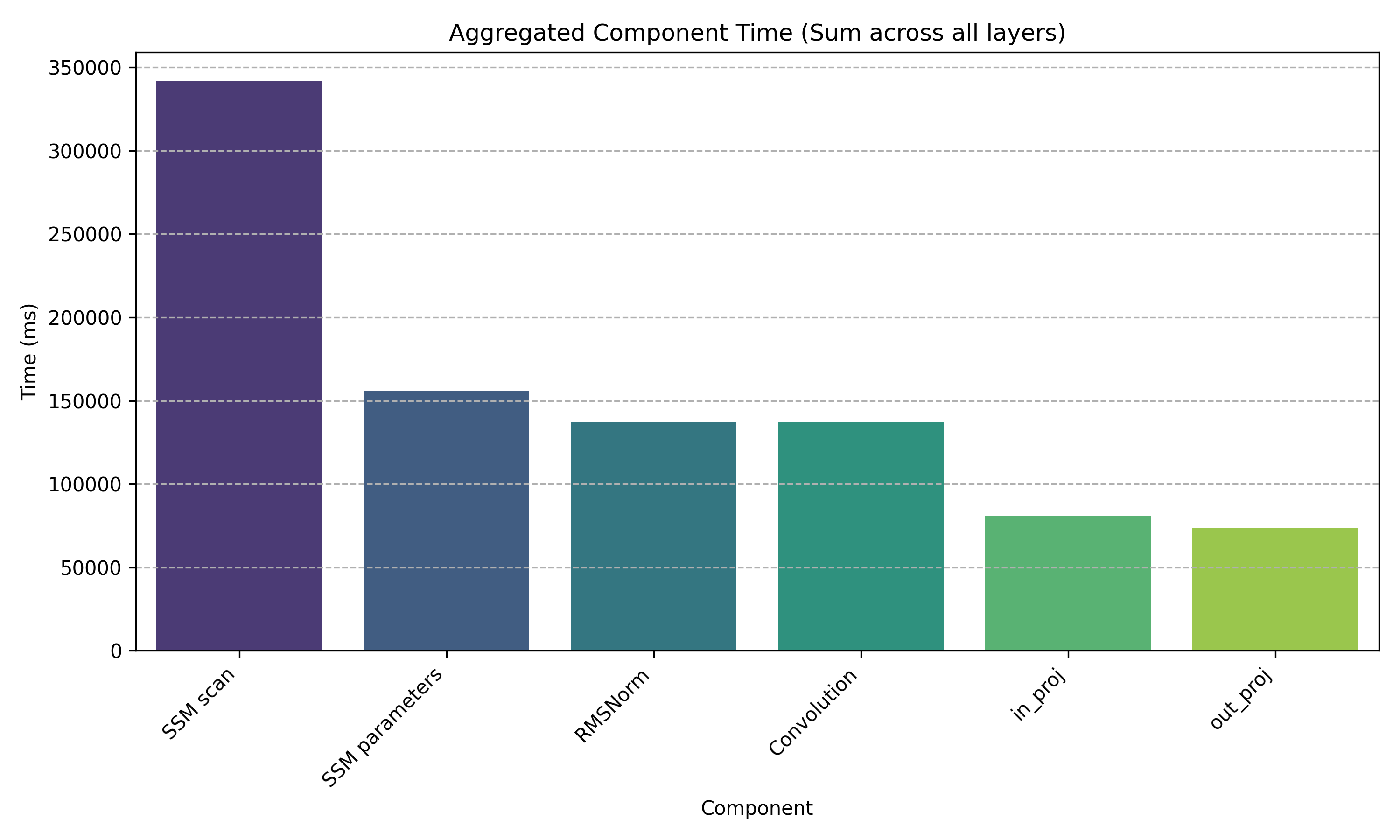
mamba MambaMixer cuda_kernels_forward

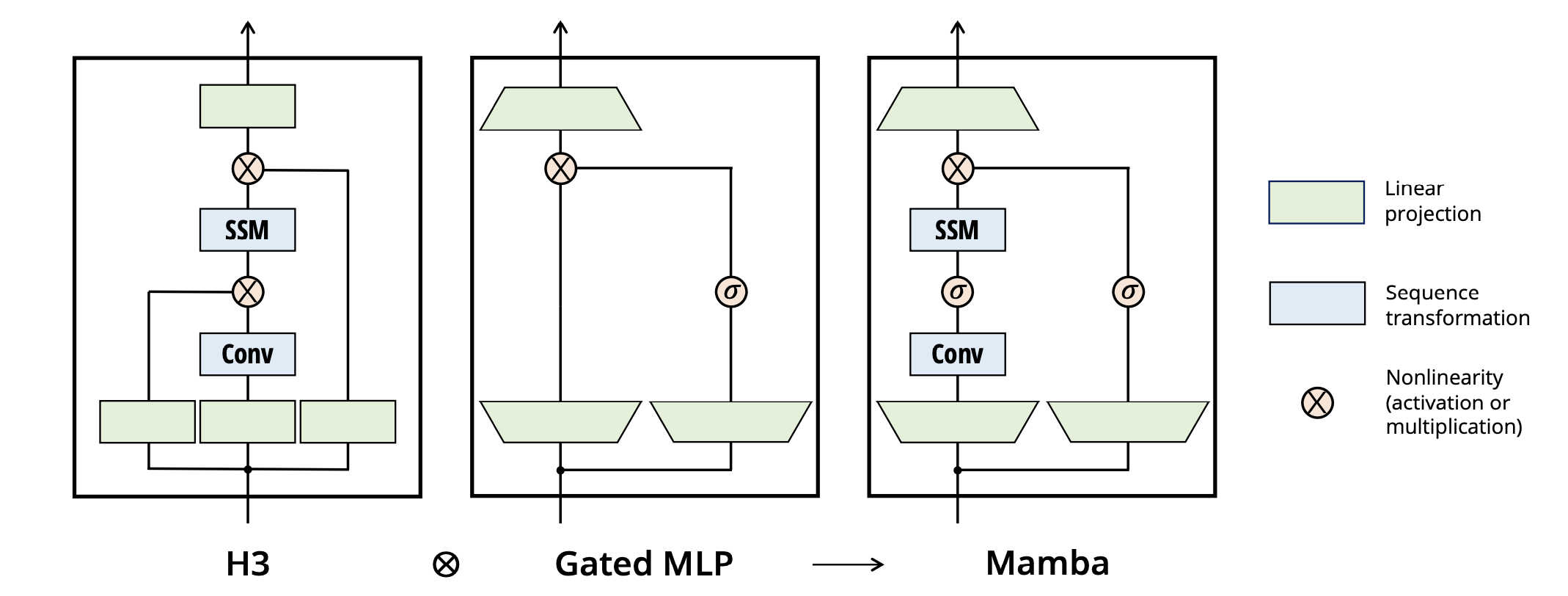
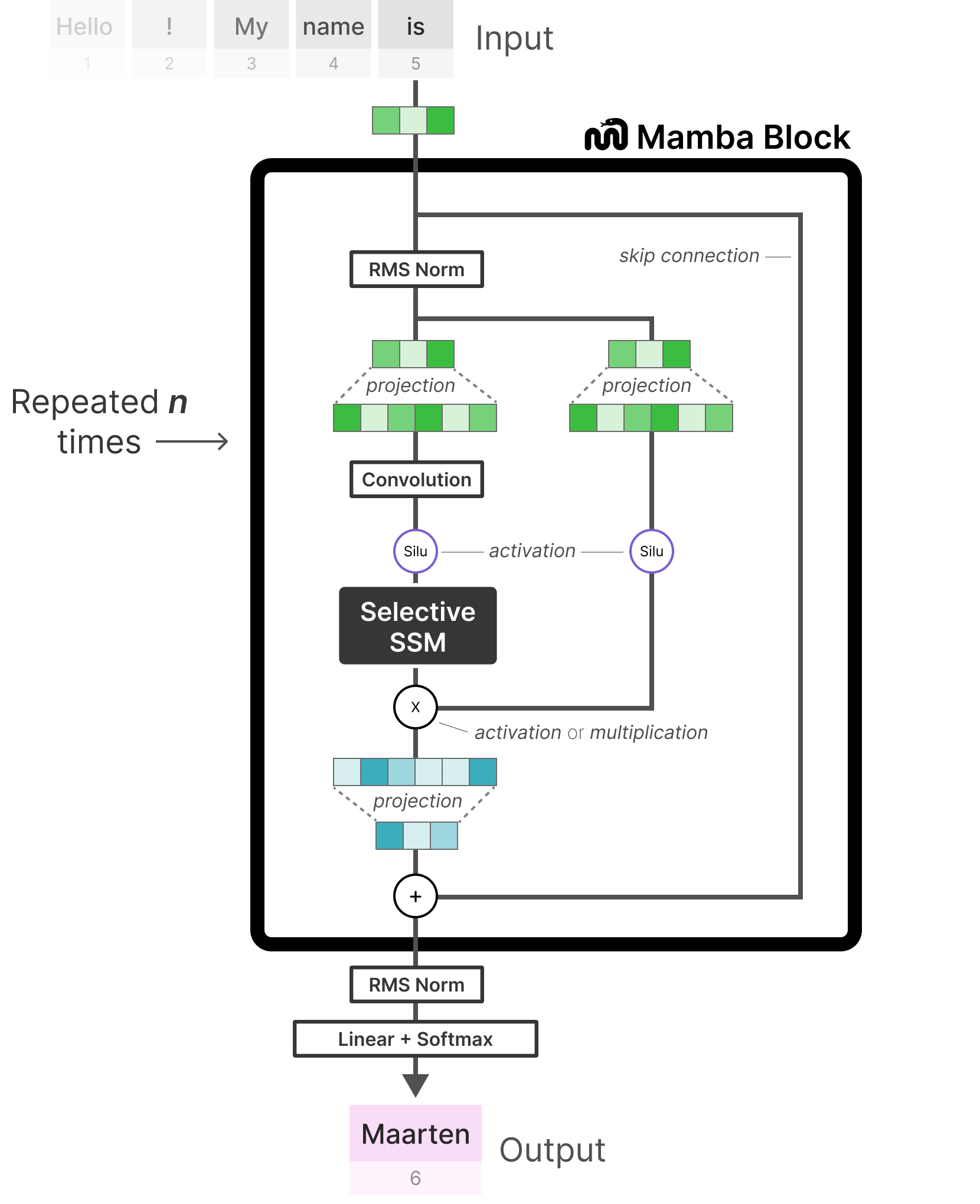
mamba block在此基础上多了一个残差连接。

residual = hidden_states
        #归一化计时
        start_event_norm = torch.cuda.Event(enable_timing=True)
        end_event_norm = torch.cuda.Event(enable_timing=True)
        start_event_norm.record()
        hidden_states = self.norm(hidden_states.to(dtype=self.norm.weight.dtype))
        end_event_norm.record()
        torch.cuda.synchronize()
        logger.info(f"[Layer {self.layer_idx}] RMSNorm time: {start_event_norm.elapsed_time(end_event_norm):.3f} ms")
        if self.residual_in_fp32:
            residual = residual.to(torch.float32)

        hidden_states = self.mixer(
            hidden_states, cache_params=cache_params, cache_position=cache_position, attention_mask=attention_mask
        )
        hidden_states = residual + hidden_states
        return hidden_states

输入hidden_states: 输入张量，形状通常为 (batch_size, seq_len, hidden_dim)，表示输入序列的隐藏状态。

1. Gated MLP 的线性投影

• 操作: 对输入 hidden_states 应用线性变换 self.in_proj，并将结果转置为 (batch_size, hidden_dim, seq_len)。
• 代码:

  projected_states = self.in_proj(hidden_states).transpose(1, 2)

• 作用: 将输入映射到更高的维度，为后续的卷积和 SSM 处理准备数据。

2. 分支：训练模式 vs 推理模式

根据是否处于训练模式（self.training）以及是否提供缓存（cache_params），函数分为两种处理路径：

训练模式（无缓存）

• 条件: self.training and cache_params is None。
• 操作: 调用 mamba_inner_fn，一次性计算整个序列的输出。
• 输入:
  • projected_states: 线性投影后的状态。
  • 卷积核权重和偏置（self.conv1d.weight, self.conv1d.bias）。
  • SSM 参数权重（self.x_proj.weight, self.dt_proj.weight, self.out_proj.weight 等）。
  • 其他超参数（如 self.A_log, self.D, delta_bias 等）。
• 输出: contextualized_states，即经过卷积和 SSM 变换后的序列。

推理模式（带或不带缓存）

推理模式下，函数逐步处理序列，支持增量计算（通过缓存）和注意力掩码。操作分为以下子步骤：

2.1 分割隐藏状态和门控

• 操作: 将 projected_states 按维度 1 分为两部分：hidden_states 和 gate。
• 代码:

  hidden_states, gate = projected_states.chunk(2, dim=1)

• 作用: hidden_states 用于后续卷积和 SSM 处理，gate 用于控制 SSM 的输出。

2.2 应用注意力掩码（可选）

• 操作: 如果提供了 attention_mask，将 hidden_states 与掩码相乘，屏蔽指定位置。
• 代码:

  if attention_mask is not None:
      hidden_states = hidden_states * attention_mask.unsqueeze(1)

• 作用: 实现类似 Transformer 的注意力机制，忽略填充或无关位置。

2.3 卷积序列变换

• 操作: 对 hidden_states 应用因果 1D 卷积（causal_conv1d_fn 或 causal_conv1d_update）。

• 分支:

  • 无缓存或首次处理 (cache_position[0] == 0):
    • 填充 hidden_states 以匹配卷积核大小。
    • 更新缓存中的卷积状态（如果有缓存）。
    • 执行完整卷积操作 causal_conv1d_fn。
  • 增量推理 (cache_position[0] > 0):
    • 使用缓存的卷积状态，执行增量卷积更新 causal_conv1d_update。

• 代码:

  conv_weights = self.conv1d.weight.view(self.conv1d.weight.size(0), self.conv1d.weight.size(2))
  if cache_params is not None and cache_position[0] > 0:
      hidden_states = causal_conv1d_update(...)
  else:
      hidden_states = causal_conv1d_fn(...)

• 作用: 通过卷积捕捉序列的局部依赖，类似于 Transformer 的局部注意力。

• 掩码: 卷积后再次应用 attention_mask（如果存在）。

2.4 状态空间模型（SSM）序列变换

SSM 是 Mamba 模型的核心，模拟序列的动态演化。分为以下子步骤：

2.4.1 输入依赖的时间步和参数初始化

• 操作: 使用 self.x_proj 投影 hidden_states，生成 SSM 参数：时间步（time_step）、输入相关矩阵 B 和 C。
• 代码:

  ssm_parameters = self.x_proj(hidden_states.transpose(1, 2))
  time_step, B, C = torch.split(ssm_parameters, [self.time_step_rank, self.ssm_state_size, self.ssm_state_size], dim=-1)
  discrete_time_step = self.dt_proj.weight @ time_step.transpose(1, 2)
  A = -torch.exp(self.A_log.float())

• 作用: 为每个输入位置生成动态的时间步和 SSM 参数，提升模型的表达能力。

2.4.2 SSM 递归计算

• 操作: 使用 SSM 公式 y ← SSM(A, B, C)(x) 更新序列。
• 参数:
  • A: 状态转移矩阵，基于 self.A_log 计算。
  • B, C: 输入依赖的矩阵，从 self.x_proj 投影和分割得到。
  • discrete_time_step: 离散化的时间步。- : 输入依赖，从 self.x_proj 的 time_step 经 self.dt_proj 投影和 Softplus 激活生成。
  • self.D: 直接传递参数。
  • gate: 控制输出的门控向量。
• 分支:
  • 增量推理 (cache_position[0] > 0):
    • 调用 selective_state_update，基于缓存的 SSM 状态更新单个时间步。
  • 完整序列:
    • 调用 selective_scan_fn，处理整个序列，并可选地返回最终 SSM 状态（用于缓存更新）。
• 代码:

  if cache_params is not None and cache_position[0] > 0:
      scan_outputs = selective_state_update(...)
  else:
      scan_outputs, ssm_state = selective_scan_fn(...)

• 作用: SSM 通过递归方式建模序列的长期依赖，相比 Transformer 更高效。
• 缓存更新: 如果有缓存，更新 SSM 状态。
• 计时: 记录 SSM 更新的推理时间。

2.5 最终线性投影

• 操作: 对 SSM 输出 scan_outputs 应用线性变换 self.out_proj，生成最终输出。
• 代码:

  contextualized_states = self.out_proj(scan_outputs.transpose(1, 2))

• 作用: 将 SSM 输出映射回原始隐藏维度，生成上下文化的序列表示。
• 计时: 记录 out_proj 的推理时间。

输出

• contextualized_states: 最终的上下文化状态，形状通常为 (batch_size, seq_len, hidden_dim)。

维度变化

假设输入 hidden_states 的形状为 (batch_size, seq_len, hidden_dim)，以下是维度的变化过程：

1. Gated MLP 投影:

   • self.in_proj: (batch_size, seq_len, hidden_dim) → (batch_size, seq_len, 2 * hidden_dim)（通常扩展为两倍维度）。
   • 转置: (batch_size, seq_len, 2 * hidden_dim) → (batch_size, 2 * hidden_dim, seq_len)。
   • 分割: 分成 hidden_states 和 gate，各为 (batch_size, hidden_dim, seq_len)。

2. 卷积变换:

   • 输入: (batch_size, hidden_dim, seq_len)。
   • 卷积后: 保持形状 (batch_size, hidden_dim, seq_len)（因果卷积不改变序列长度）。

3. SSM 变换:

   • 输入: (batch_size, hidden_dim, seq_len)。
   • x_proj: 生成 ssm_parameters，形状为 (batch_size, seq_len, time_step_rank + 2 * ssm_state_size)。
   • 分割为 time_step (time_step_rank)，B 和 C（各 ssm_state_size）。
   • dt_proj: time_step → (batch_size, hidden_dim, seq_len)。
   • SSM 输出: (batch_size, hidden_dim, seq_len)（selective_scan_fn 或 selective_state_update）。

4. 最终投影:

   • 转置: (batch_size, hidden_dim, seq_len) → (batch_size, seq_len, hidden_dim)。
   • self.out_proj: (batch_size, seq_len, hidden_dim) → (batch_size, seq_len, hidden_dim)（输出维度通常与输入一致）。

ssm与其它序列模型的比较

(1) RNN（循环神经网络）

• 基本结构：
  

  • 通过隐藏状态 传递历史信息。
  • 使用 简单非线性激活（如 tanh） 更新状态。

• 问题：

  • 梯度消失/爆炸：难以学习长距离依赖。
  • 顺序计算：无法并行训练。

(2) LSTM（长短期记忆网络）

• 改进点：引入 门控机制（输入门、遗忘门、输出门） 控制信息流：
  $$
  \begin{aligned}
  f_t &= \sigma(W_f [h_{t-1}, x_t] + b_f) \quad &\text{(遗忘门)} \
  i_t &= \sigma(W_i [h_{t-1}, x_t] + b_i) \quad &\text{(输入门)} \
  o_t &= \sigma(W_o [h_{t-1}, x_t] + b_o) \quad &\text{(输出门)} \
  \tilde{C}t &= \tanh(W_C [h{t-1}, x_t] + b_C) \quad &\text{(候选记忆)} \
  C_t &= f_t \odot C_{t-1} + i_t \odot \tilde{C}_t \quad &\text{(记忆更新)} \
  h_t &= o_t \odot \tanh(C_t) \quad &\text{(输出)}
  \end{aligned}
  $$

• 优势：

  • 比普通 RNN 更能捕捉长距离依赖。
  • 通过门控缓解梯度消失问题。

• 局限：

  • 仍依赖 顺序计算，训练速度慢。
  • 长序列下可能仍会丢失早期信息。

(3) SSM（结构化状态空间模型）

• 核心思想：

  • 受控于连续时间状态空间方程，离散化后处理序列：
    
  • 通过 结构化参数（如对角矩阵） 约束 ，提升计算效率。

• 优势：

  • 线性复杂度（O(N)），适合超长序列。
  • 训练时可并行（通过卷积或并行扫描）。
  • 推理时可递推（类似RNN），内存占用低。

---

** 关键区别总结**

特性	RNN	LSTM	SSM（如S4/Mamba）
长序列建模能力	❌ 梯度消失	✅ 优于RNN	✅ 最优（理论无限上下文）
训练并行性	❌ 顺序计算	❌ 顺序计算	✅ 卷积/并行扫描
计算复杂度	O(N)	O(N)	O(N)
推理模式	递推	递推	可递推或并行
参数效率	低	较高（门控机制）	高（结构化参数）
典型应用	短序列任务	文本、语音	超长序列（DNA、音频、时间序列）

ssm的并行性

SSM（状态空间模型）在并行计算中依赖快速傅里叶变换（FFT）。FFT是计算卷积的最优工具之一，尤其在处理长序列时。

1. SSM与卷积的等价性

在现代SSM实现中，状态空间模型可以通过数学推导重写为卷积形式。具体来说，SSM的状态更新方程：

• 
  可以展开为一个输入序列 与一个由 、、 参数生成的卷积核 的卷积：
• 
  这里的 是一个由状态空间参数决定的核函数（例如，）。这意味着，SSM的输出可以看作输入序列与某个固定核的卷积结果。

2. 卷积的直接计算复杂度高

如果直接计算这个卷积，对于长度为 的序列，时间复杂度是 ，因为每个输出 需要对输入序列的 个元素与核 进行加权求和。当序列很长时（比如 在千或万级别），这种朴素计算方式在时间和计算资源上都非常昂贵，无法高效并行。

3. FFT加速卷积

快速傅里叶变换（FFT）提供了一种高效计算卷积的方法。根据卷积定理：

• 时域中的卷积等价于频域中的点乘。
• 即 可以通过 计算，其中 表示傅里叶变换， 表示逆傅里叶变换。

使用FFT的步骤如下：

1. 将输入序列 和核 转换为频域： 和 ，复杂度为 。
2. 在频域中进行逐元素乘法：，复杂度为 。
3. 将结果转换回时域：，复杂度为 。

总复杂度降为 ，远低于直接卷积的 。

4. 并行化的实现

• 频域计算的独立性：在频域中，每个频率分量的乘法是独立的，可以在GPU等并行硬件上同时计算。
• 批量处理：FFT本身是一个高度优化的算法，现代硬件和库（如cuFFT）能够一次性处理整个序列的变换，进一步提升并行效率。
• 全局操作：通过FFT，SSM不再需要按时间步顺序递归计算，而是将整个序列的卷积一次性完成，消除了时间依赖性，天然适合并行化。

5. Ssm推理训练不同方式

Commonly, the model uses the convolutional mode (3) for efficient parallelizable training (where the whole input sequence
is seen ahead of time), and switched into recurrent mode (2) for efficient autoregressive inference (where the inputs are
seen one timestep at a time).

(Mamba: Linear-Time Sequence Modeling with Selective State Spaces)此处model代之Structured state space sequence models (S4)

附ssm公式推导

，因为机器学习中的序列数据是离散的，而原始SSM通常以连续形式定义。从连续形式 求解并离散化，得到离散形式 。

1. 连续微分方程

SSM的连续形式为：

• 状态更新：
  
  其中：

  • 是隐状态向量（随时间 连续变化）。
  • 是状态对时间的导数。
  • 是状态转移矩阵（通常是方阵）。
  • 是输入矩阵。
  • 是输入（可以是标量或向量）。

• 输出：
  
  （这里我们主要关注状态更新方程的离散化，输出部分直接应用离散后的状态）。

这是一个一阶线性常微分方程（ODE），我们需要求解 的解析解，然后将其离散化。

---

2. 求解连续微分方程

为了离散化，我们首先需要求解这个ODE的通解。假设初始条件为 ，输入 是已知的。

(1) 齐次方程的解

先考虑齐次情况（无输入项，即 ）：

这是一个标准的线性齐次ODE，其解为：

其中 是矩阵指数，定义为：

这是状态的自然演化，受初始条件 和矩阵 控制。

(2) 非齐次方程的解

现在加入输入项 ，完整的方程是：

非齐次线性ODE的通解是齐次解加上特解。使用变分常数法求解：

• 假设特解形式为 ，其中 是待定函数。

• 代入原方程：
  
  
  得到：
  
  两边消去 ：
  
  

• 积分求 ：
  
  （ 是常数，由初始条件决定）。

• 代回特解：
  

• 通解：
  
  调整积分项：
  
  （通过变量替换 可验证等价性）。

通解公式

最终，连续SSM的状态解为：

• 第一项：初始状态随时间演化。
• 第二项：输入 在时间区间 内的累积影响。

---

3. 离散化：零阶保持（ZOH）

在离散时间序列中，假设时间步长为 ，输入 在每个区间 内是常数（即 ），我们需要计算 。

设置时间点

• ，，，…，。
• 初始状态 。
• 目标：求 、 等。

计算

令 ，：

假设 （常数，零阶保持假设）：

积分计算

令 ，则 ，积分限从 到 变为 到 ：

因为 是常数，提出积分外：

计算积分：

（假设 可逆，若不可逆则需用伪逆或更广义形式）。
因此：

离散递推

定义：

• （离散状态转移矩阵）
• （离散输入矩阵）

则：

推广到任意时间步：

---

4. 离散化公式

最终离散化的SSM为：

• 状态更新：
  
• 输出：
  
  其中：

---

5. 注意事项

• **步长 **：在S4、Mamba等模型中， 可以是可学习的参数，动态调整离散化精度。
• **矩阵指数 **：实际计算中通过数值方法（如对角化或Pade近似）实现。
• **不可逆 **：若 不可逆， 的定义需调整，通常直接参数化 和 而非严格依赖 。

---

总结

离散化SSM的求解过程：

1. 从连续方程 出发，求通解：
   
2. 假设输入在每个时间步内常数（ZOH），计算 ：
   
3. 提取离散参数 和 ，得到递归形式：