KV Cache and MLA

Ikko Lv3
  2025-03-26 14:15:55 2025-03-26 14:15:55 Created   2025-03-28 10:26:49 2025-03-28 10:26:49 Updated  2.3k Words  8 Mins  

在 Decoder-only 的 Transformer 模型（如 GPT、DeepSeek-V3） 中，KV Cache 的核心作用正是为了 避免重复计算历史 token 的 Key 和 Value，从而实现高效的自回归生成。

背景 自回归attention机制

1. 核心分工

组件 角色 自回归中的关键设计
Query (Q) 当前Token的“问题” 仅由最新生成的Token计算（）
Key/Value (K/V) 历史信息的“答案库” 缓存所有历史Token的K/V（）
Attention机制 Q与历史K/V交互 通过因果掩码确保仅访问历史信息

2. 具体实现方式

(1) Query (Q) 的来源
  • 始终由当前输入Token生成（即上一步预测出的的隐藏状态）。
  • 计算方式：
    • 例如：生成第3个Token时，Q仅来自x₂的隐藏状态。
(2) Key/Value (K/V) 的来源
  • 缓存所有历史Token的K/V（包括刚计算的）：
    • 例如：生成第3个Token时，包含 ₁ 和 ₂的信息。
(3) 注意力交互
  • Q与历史K/V计算相似度：
    • 由于因果掩码，不会与未来的等交互（尽管此时未来信息尚未生成）。

3. 为什么这样设计？

  • 数学一致性：
    自回归要求 ，即当前Token仅依赖历史信息。通过限制只与历史交互实现这一点。

  • 计算效率：

    • 只需计算当前Token，避免冗余。
    • 缓存历史信息，避免重复计算。

  • 灵活性与泛化性：
    作为“当前问题的提出者”，动态决定需要关注历史的哪些部分（通过Attention权重）。

4. 对比图示

1
2
3
4
5
生成第3个Token (x₃) 时的数据流：
Step 1: x₂ → Q₃ (仅当前)
              ↓
Step 2: Q₃ → [K₁, K₂] → Attention → 加权求和 → 输出
              [V₁, V₂]
  • **₃**：由₂的隐藏状态计算，代表“当前需要什么信息”。
  • **₁₂ / ₁₂**：历史信息的编码，代表“已知的信息库”。

5. 常见误区澄清

  • ❌ 误区：“Q也需要包含所有历史Token。”
    ✅ 正解：Q仅来自当前Token，历史信息由K/V提供。
  • ❌ 误区：“因果掩码直接作用于Q。”
    ✅ 正解：掩码作用于Q与K的交互矩阵，确保Q不访问未来的K。

总结

  • 是“提问者”：由当前Token动态生成，决定关注哪些历史信息。
  • 是“记忆库”：缓存所有历史Token的信息，供Q查询。
  • 因果性保障：通过Q与历史K/V的交互 + 掩码，严格实现自回归的数学定义。

这种分工使得Transformer在生成时既能高效利用历史信息，又能保持自回归的特性。

1. KV Cache 的复用机制

(1) 每次生成新 token 时的计算流程

当模型生成第 个 token 时：

  1. 当前 token 的 Query（）：
    • 由当前 token 的隐藏状态计算（新计算，无法复用）。
  2. 历史 token 的 Key/Value（、）：
    • 直接复用 KV Cache 中缓存的结果，无需重新计算。
    • 新生成的 、 会追加到缓存中供后续使用。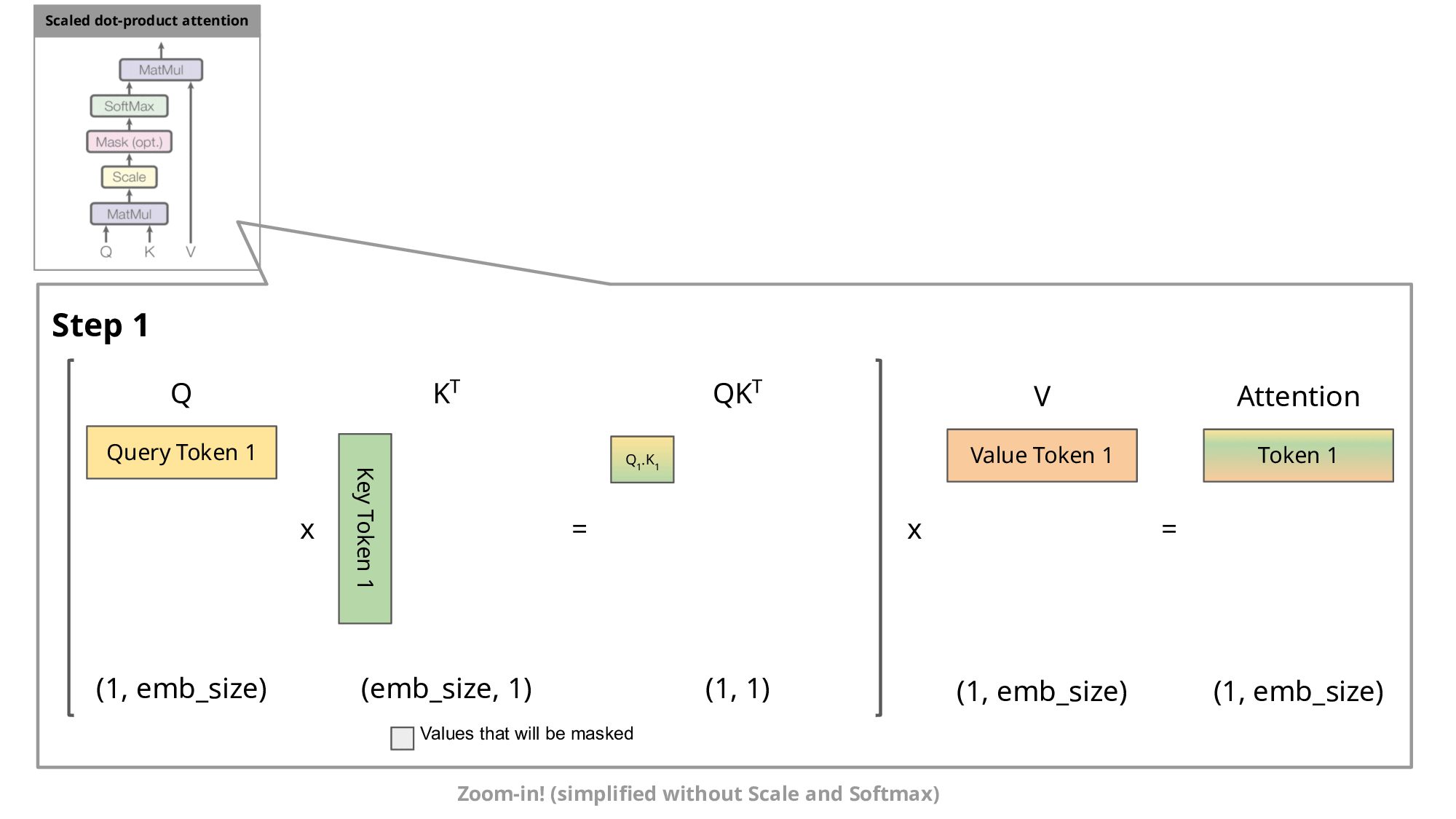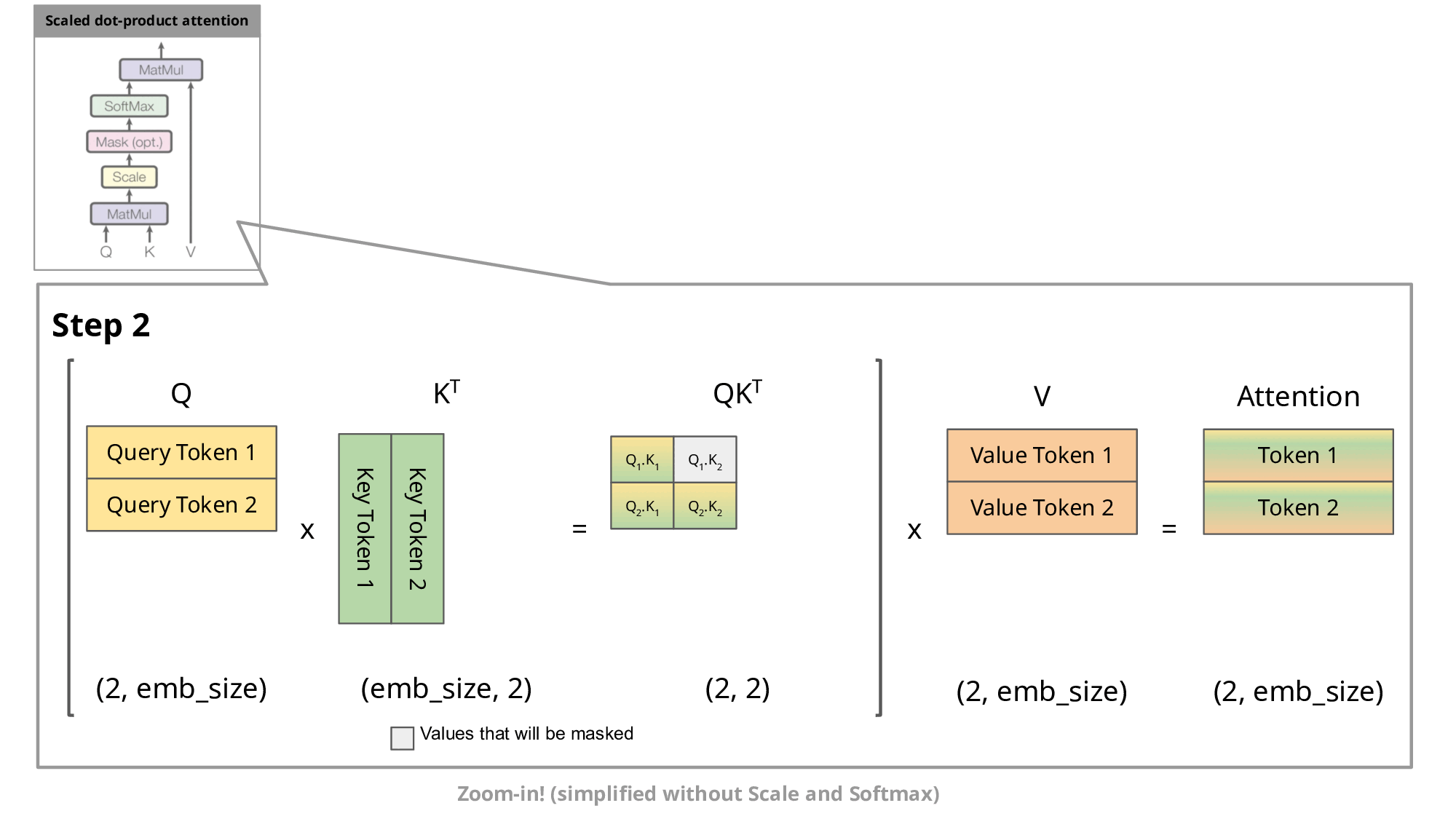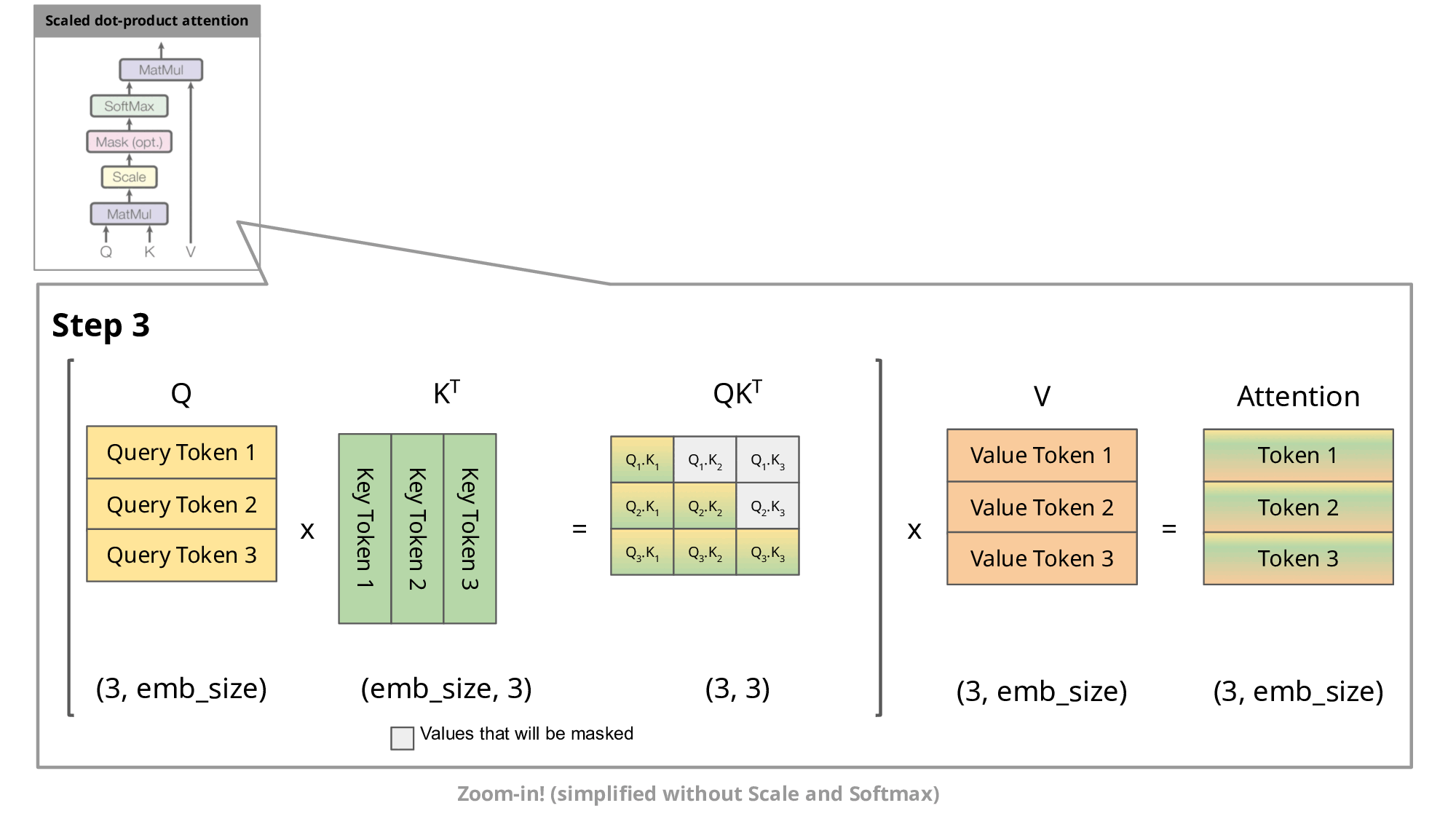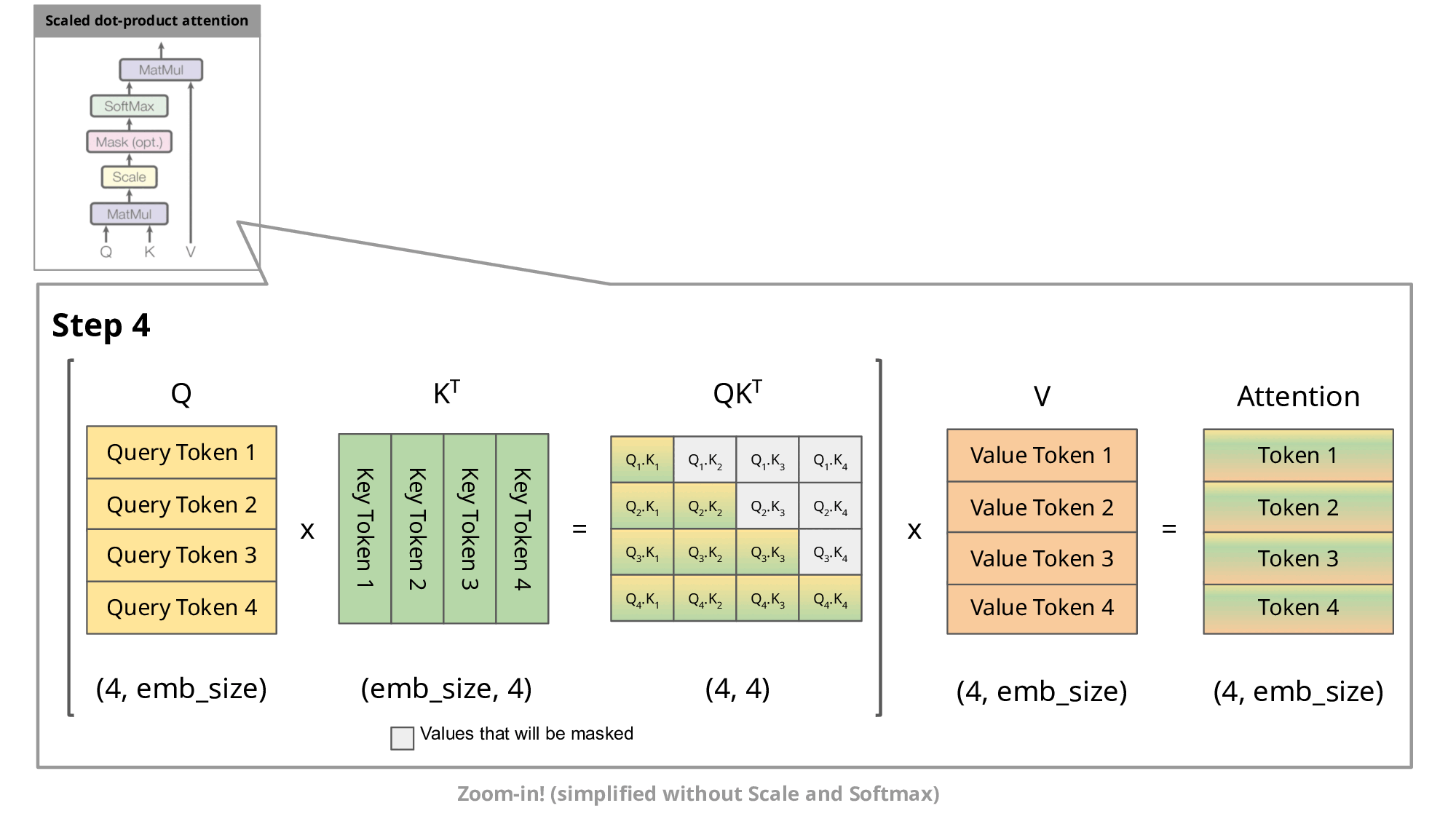
      kv cache(图源https://medium.com/@joaolages/kv-caching-explained-276520203249)

(2) 注意力计算的具体步骤

  • 复用部分：
    和 直接读取自缓存，仅 、 需新计算。
  • 计算量节省：
    避免了为每个新 token 重新计算所有历史 token 的 K/V，将复杂度从 降至 。

2. 为什么能复用？

(1) 自回归生成的特性

  • 单向依赖性：生成第 个 token 时，模型仅依赖之前所有 token（1 到 ）的信息，历史 token 的 K/V 不会改变。
  • 静态性：历史 token 的隐藏状态（及投影后的 K/V）在生成过程中是固定的，无需更新。

(2) 投影矩阵的确定性

  • 每层的 、 是固定的，因此同一 token 的 K/V 只需计算一次即可复用：

    其中 是第 个 token 的隐藏状态。

3. KV Cache 的存储与更新

(1) 存储结构

  • 每层独立缓存：
    每个 Decoder 层维护自己的 KV Cache，存储该层所有历史 token 的 和 。
  • 形状示例：
    对于 层模型、序列长度 、头数 、头维度 ：
    大小

(2) 更新逻辑

1
2
3
4
5
6
7
8
9
10
11
12
13
# 伪代码示例：生成第 t 个 token 时的 KV Cache 更新
for layer in decoder_layers:
    # 计算当前 token 的 K_t, V_t
    K_t = current_hidden_state @ W_K  # [n_h, d_h]
    V_t = current_hidden_state @ W_V  # [n_h, d_h]
    
    # 追加到该层的 KV Cache
    layer.kv_cache.keys.append(K_t)    # 形状变为 [n_h, t, d_h]
    layer.kv_cache.values.append(V_t)
    
    # 注意力计算：Q_t 与所有历史 K/V 交互
    attn_scores = Q_t @ concat(K_1, ..., K_t).T  # 复用缓存的 K_1...K_{t-1}
    output = attn_scores @ concat(V_1, ..., V_t)  # 复用缓存的 V_1...V_{t-1}

Multi-head Latent Attention (MLA) 是 DeepSeek-V2 中提出的一种创新的注意力机制，旨在解决传统注意力机制在推理效率上的瓶颈问题，特别是 Key-Value (KV) 缓存的高内存占用问题。
MLA 的目标是：

  • 保持高性能：性能优于 MHA。
  • 显著减少 KV 缓存：通过低秩压缩技术降低存储需求。

2. MLA 的核心设计

MLA 的核心创新是 低秩 Key-Value 联合压缩 和 解耦的旋转位置编码。

(1) 低秩 Key-Value 联合压缩

  • 压缩过程：
    1. 将 Key 和 Value 投影到一个低维的共享潜在向量 $(\mathbf{c}{t}^{\text{KV}}：$
      \mathbf{c}      {t}^{\text{KV}} = W^{DKV} \mathbf{h}_t
      $$
      其中 )（例如 )，而 )）。
    2. 通过上投影矩阵 ) 和 ) 从 ) 恢复 Key 和 Value：
      $$
      \mathbf{k}t^C = W^{UK} \mathbf{c}{t}^{\text{KV}}, \quad \mathbf{v}t^C = W^{UV} \mathbf{c}{t}^{\text{KV}}
      $$
  • 推理优化：
    • 只需缓存低维的 )（而非完整的 Key 和 Value），显著减少缓存需求。
    • 通过矩阵乘法的结合律，将 ) 和 ) 吸收到 Query 和输出投影矩阵中，避免重复计算。

(2) 解耦的旋转位置编码 (RoPE)

  • 问题：传统的 RoPE 直接应用于 Key 和 Query，导致位置敏感的矩阵无法在推理时被吸收，需实时计算 Key。
  • 解决方案：
    • 引入额外的解耦 Query ) 和共享 Key ) 来承载 RoPE：
    • 将压缩的 Key/Value 与解耦的 RoPE Key 拼接后计算注意力：
    • 推理时只需额外缓存 )，进一步减少计算开销。

3. KV 缓存对比

MLA 的 KV 缓存需求显著低于传统方法：

  • MHA：需缓存 ) 个元素（例如 860.2K）。
  • MLA：仅需缓存 ) 个元素（例如 34.6K，为 MHA 的 4%）。
  • 性能：在相同参数量下，MLA 表现优于 MHA（如表 9 所示）。

4. 优势

  1. 高效推理：
    • 减少 93.3% 的 KV 缓存，支持更大的批处理量和更长的上下文（128K）。
    • 吞吐量提升 5.76 倍（相比 DeepSeek 67B）。
  2. 性能提升：
    • 通过低秩压缩和解耦 RoPE，保持更强的表达能力。
  3. 训练经济性：
    • 激活参数仅 21B（总参数 236B），节省 42.5% 训练成本。

5. 公式总结

MLA 的完整计算流程如下：

  1. Query 压缩（可选）：
  2. Key-Value 压缩：
  3. 解耦 RoPE：
  4. 注意力计算：
    $$
    \mathbf{o}{t,i} = \sum{j=1}^t \text{Softmax}\left(\frac{[\mathbf{q}{t,i}^C; \mathbf{q}{t,i}^R]^T [\mathbf{k}_{j,i}^C; \mathbf{k}j^R]}{\sqrt{d_h + d_h^R}}\right) \mathbf{v}{j,i}^C
    $$

6. 应用与意义

MLA 是 DeepSeek-V2 实现高效推理的核心技术之一，尤其适合：

  • 长上下文场景（如 128K 文本处理）。
  • 资源受限部署（如减少显存占用）。
  • MoE 模型：与 DeepSeekMoE 结合，平衡稀疏激活与计算效率。

附录

ROPE

原始 Transformer 的位置编码设计

在原始 Transformer 中，注意力机制本身不具备感知 token 位置的能力，因此需要显式地引入位置信息。Vaswani 等人选择了一种简单而有效的方案——正弦位置编码，其设计基于以下考虑：

(1) 绝对位置编码
  • 实现方式：正弦位置编码通过正弦和余弦函数为每个 token 的位置生成一个固定向量。具体公式为：

    其中 是 token 的位置， 是嵌入维度的索引， 是模型的嵌入维度。
  • 特点：这种编码为每个位置分配一个唯一的向量，与 token 的词嵌入相加后输入到模型中。
(2) 无参数设计
  • 原因：正弦位置编码不需要训练任何参数，完全由数学公式生成。这减少了模型的复杂性，并避免了因位置编码引入额外的可学习参数。
  • 优势：在当时，这种方法简单高效，且适用于任意长度的序列（理论上），因为位置向量可以按需计算。

RoPE(Rotary Position Embedding,旋转位置编码)详解

RoPE 是一种用于 Transformer 的位置编码方法，由苏剑林等人提出(论文《RoFormer: Enhanced Transformer with Rotary Position Embedding》)。它的核心思想是通过旋转矩阵将位置信息融入 Query 和 Key 的向量中，从而在不增加显式位置编码的情况下，实现对序列位置的建模。

RoPE 的核心原理
(1) 数学形式

对于位置为 的 token,其 Query 或 Key 向量 通过旋转矩阵 进行变换：

其中旋转矩阵 是一个分块对角矩阵，每个子矩阵对向量的二维分量施加旋转：

参数 控制旋转频率，通常设置为 。

(2) 特点
  • 相对位置感知：通过旋转角度的差值 ，模型能自然学习相对位置关系。
  • 长程衰减性：高频旋转分量（大 ）对远距离位置的依赖减弱，符合语言建模的局部性先验。
  • 无需显式拼接位置编码：直接修改 Query 和 Key 的值，节省计算和存储。
  • Title: KV Cache and MLA
  • Author: Ikko
  • Created at : 2025-03-26 14:15:55
  • Updated at : 2025-03-28 10:26:49
  • Link: http://ikko-debug.github.io/2025/03/26/MLA/
  • License: This work is licensed under CC BY-NC-SA 4.0.
Comments
On this page
KV Cache and MLA
  1. 背景 自回归attention机制
  2. 1. KV Cache 的复用机制
  3. 2. 为什么能复用？
  4. 3. KV Cache 的存储与更新
  5. 2. MLA 的核心设计
  6. 3. KV 缓存对比
  7. 4. 优势
  8. 5. 公式总结
  9. 6. 应用与意义
  10. 附录
  11. RoPE(Rotary Position Embedding,旋转位置编码)详解