信号与系统

常用英文

even，odd 偶数，奇数
exponential 指数
sinusoidal 正弦
series (cascade) interconnection 串联级联
parallel interconnection 并联
series-parallel interconnection 串并联
differential equation 微分方程
rational function 有理函数
block diagram representation 框图表示
convolution integral 卷积积分
converge 收敛
finite duration 有限长
corrseponding magnitude，phase response 对应的幅度，相位响应

坐标轴偏移

平移考虑系数，缩放考虑偏移量,考虑自变量系数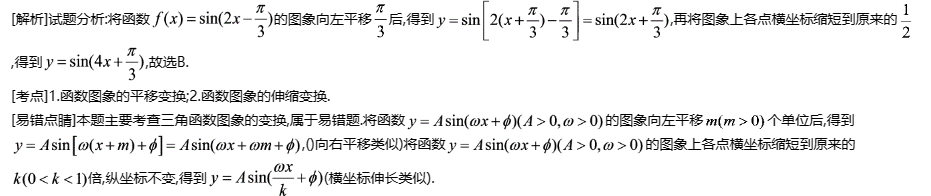


任何一个函数都能表示成一个偶函数和一个奇函数的和。

properties

脉冲函数和跃迁函数

离散

连续

他们俩是求导和积分的关系
间断点值取两边极限的平均值

电容

C=Q/U
I=C*dU/dt

时变时不变系统(time-varying and time-invariant systems)

一个是平移运算，一个是往x(t)代入
首先，我们来分析系统的时变与时不变性。

1. 系统

考虑输入 。对此输入，其输出为：

若系统是时不变的，那么对于 的输出应该是 ，即：

因为 ，所以该系统是时变的。

2. 系统

考虑输入 。其输出为：

若系统是时不变的，那么对于 的输出应该是 ，即：

由于 ，所以该系统是时不变的。

3. 系统

考虑输入 。其输出为：

若系统是时不变的，那么对于 的输出应该是 ，即：

由于 ，所以该系统是时不变的。

结论：在这三个系统中，第一个是时变的，而后两个是时不变的。
y(t)=x(t-2)+x(2-t)是时变的
输入x(t-a)输出为 y(t-a)=x(t-2-a)+x(2-t-a)
对于y(t-a),输出y(t-a)=x(t-2-a)+x(2-t+a)

可逆和不可逆系统（invertibility and non-inverse systems）

如何证明一个系统不可逆：
对于给定的输出，可能有多个不同的输入能够产生相同的输出，这意味着从输出中无法确定一个唯一的输入。

以下是证明一个系统不可逆的一般方法：

找到两个不同的输入：首先，我们需要找到两个不同的输入信号，这两个信号在经过系统处理后产生相同的输出。

展示相同的输出：然后，我们需要显示这两个不同的输入信号经过系统处理后确实产生相同的输出。

结论：一旦我们展示了两个不同的输入可以产生相同的输出，我们就证明了该系统是不可逆的，因为从输出中无法唯一确定输入。

线性和非线性系统（linear and nonlinear systems）

易错：

因果和非因果系统（causal and non-causal systems）

证明一个系统是非因果的通常涉及到检查其因果性质，也就是系统的输出不能依赖于未来的输入值。
找到一个具体的反例：首先，需要找到一个具体的输入信号和相应的输出，使得输出信号在某些时刻依赖于未来的输入值。这是非因果性的典型标志。

稳定和不稳定系统（stable and unstable systems）

给定定义域自变量，输出为有限值。

一道关于ut的卷积题

所以


因为t≥0，为了满足这个条件，所以乘了u(t)

矩形函数卷积

ht物理意义就是输入为δt时的yt

初始松弛

线性时不变（LTI）系统满足初始松弛（Initial Rest）的条件意味着，当输入为零时，输出也为零，至少在一开始是这样的。更明确地说，对于所有的t＜0，如果x(t)=0 （即系统的输入为零），那么输出 y(t)=0。

关于脉冲函数的一些公式

特殊：

傅里叶级数

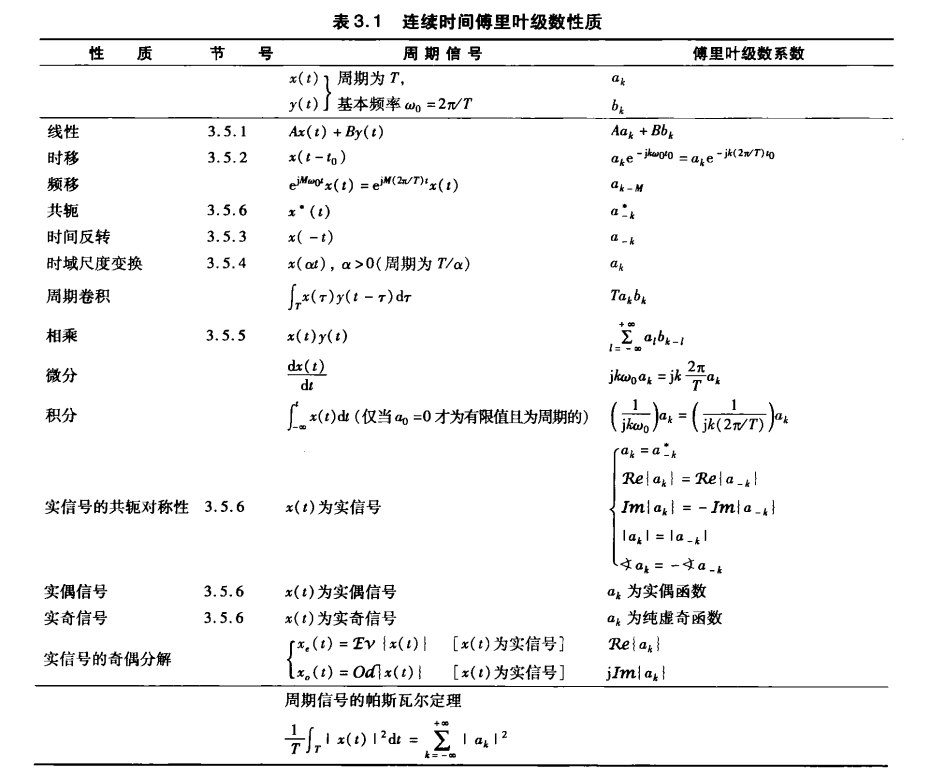
连续时间傅里叶变换

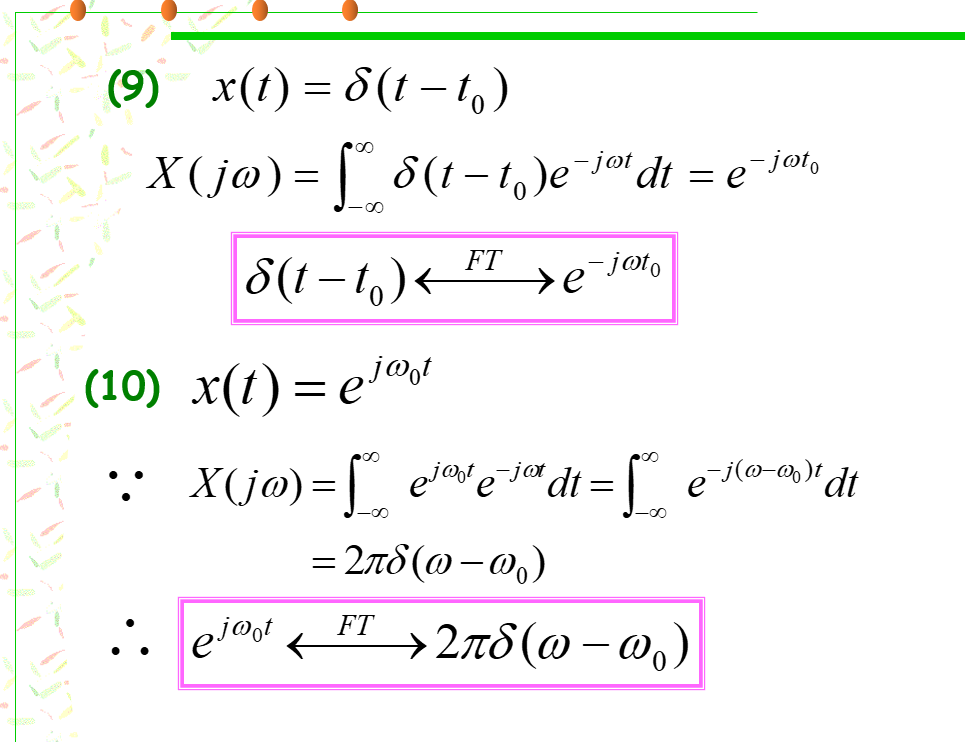
so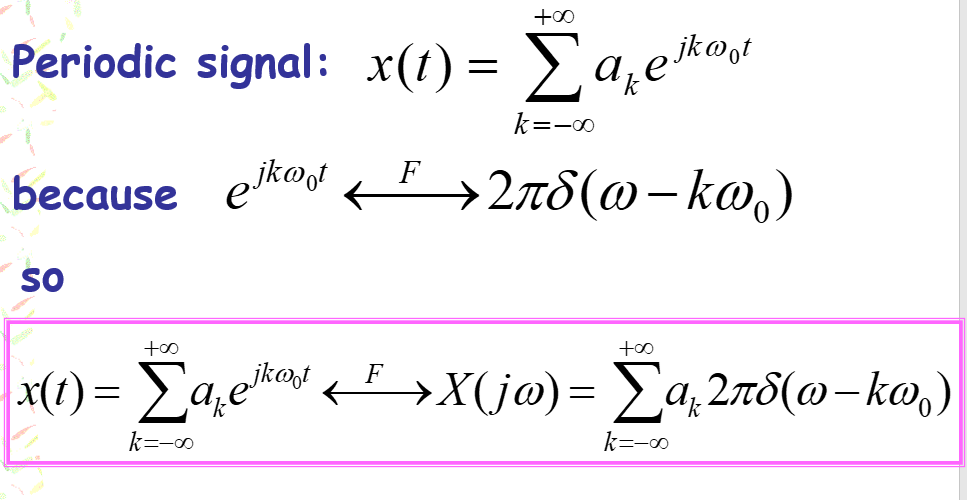

常用变换对

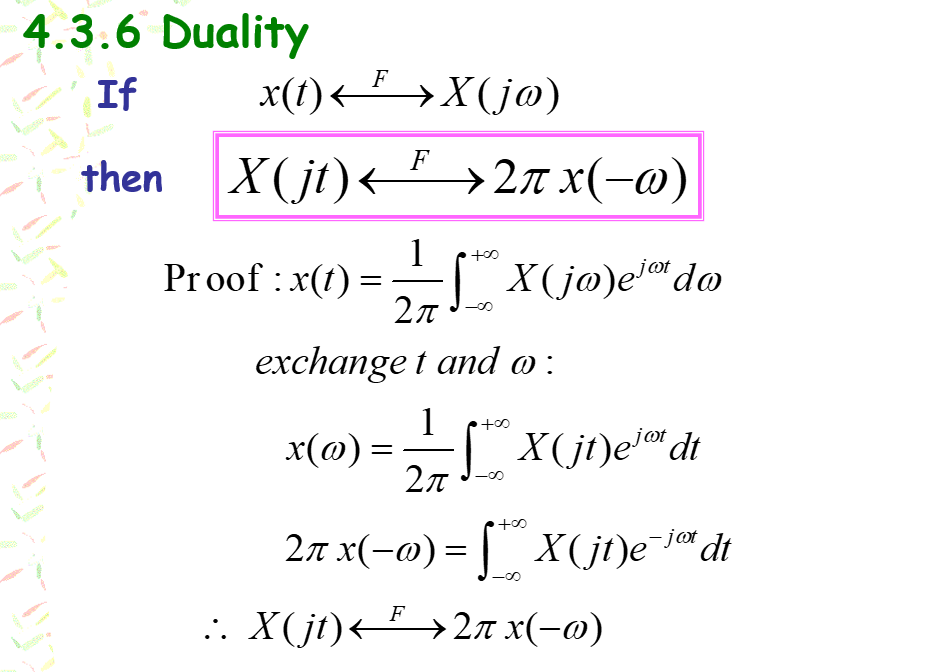
求傅里叶变换：t换w，再乘2Π

傅里叶变换性质

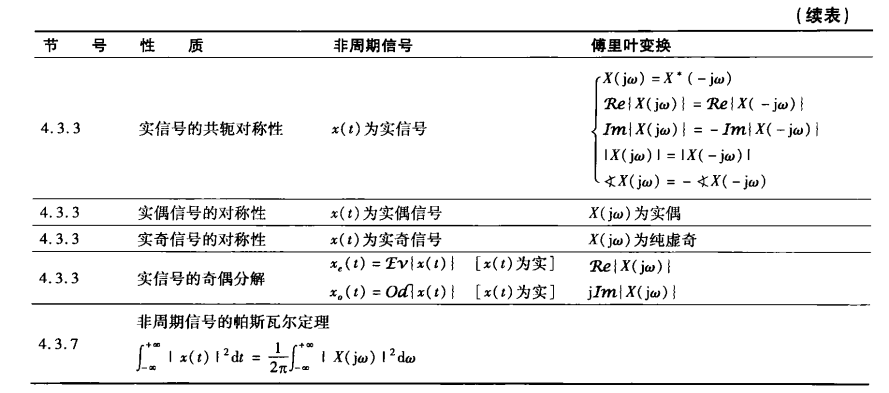
常用傅里叶变换对

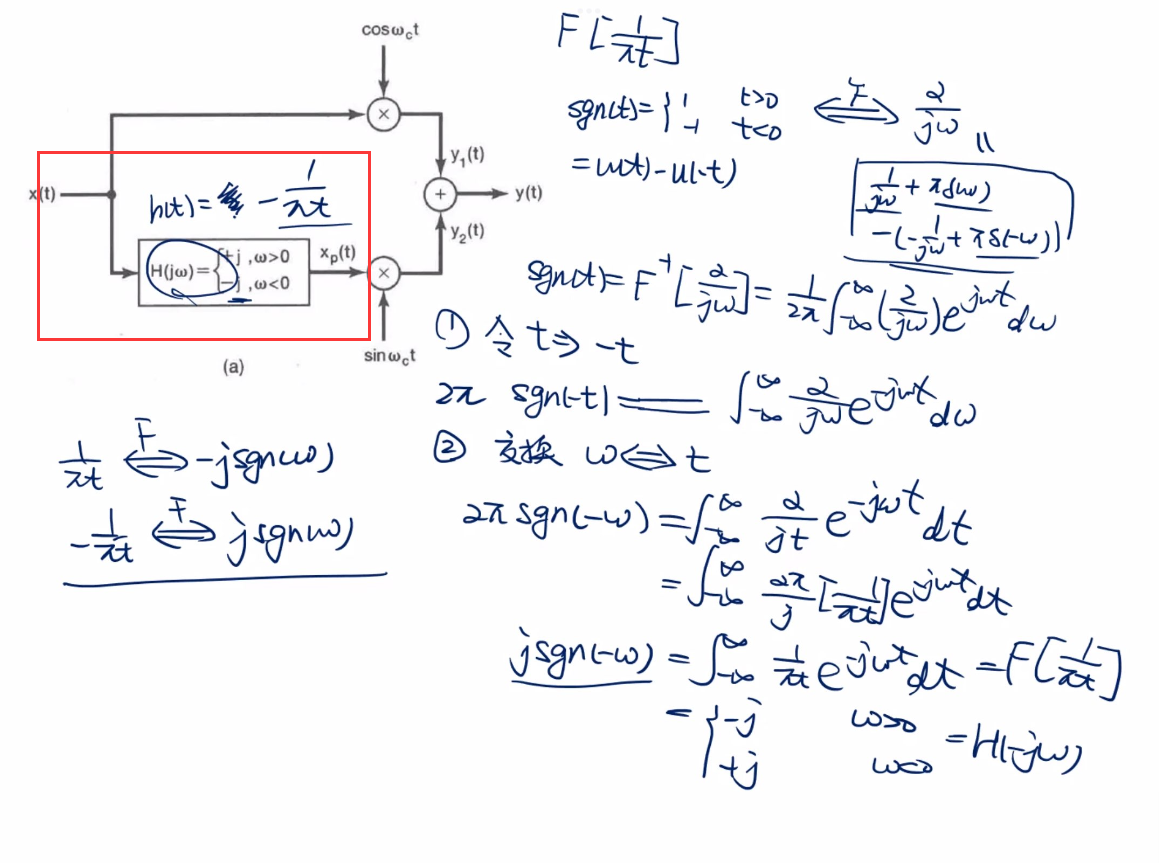
易不会的题

求微分方程

重要公式

奈奎斯特采样定理

奈奎斯特采样定理是数字信号处理中的一个重要定理，它规定了对于一个带限信号，为了能够完全恢复原始信号，采样频率必须大于信号最高频率的两倍。
具体来说，奈奎斯特采样定理指出，如果一个连续时间信号的最高频率为fmax，那么它应该以不低于2fmax的采样频率进行采样，才能够在离散时间中完全还原原始信号。
这个定理的重要性在于，如果采样频率低于奈奎斯特频率，就会出现采样失真，即原始信号的高频成分会被混叠到低频区域，导致无法准确还原原始信号。
因此，奈奎斯特采样定理在数字信号处理中具有重要的指导意义，它保证了采样后的信号能够准确地表示原始信号，并为后续的信号处理提供了基础。

群时延

零阶保持采样方法

零阶保持采样是一种常见的数字信号处理方法，主要用于将连续时间信号转换为离散时间信号。其基本思想是在每个采样点上，将信号的值保持不变，直到下一个采样点。

以下是零阶保持采样的基本步骤：

在指定的采样率下，选择连续时间信号的采样点。
在每个采样点上，记录信号的值。
在两个采样点之间，将信号的值保持为前一个采样点的值。
这种方法的一个主要优点是它简单易实现。然而，它也有一些缺点。例如，它可能会引入一些误差，因为它假设信号在两个采样点之间是恒定的，而实际上信号可能会有变化。此外，如果采样率不够高，它可能会错过信号的一些重要特征。

在实际应用中，零阶保持采样通常用于数据转换器（DACs）和模拟-数字转换器（ADCs）等设备，以将数字信号转换为模拟信号，或者反过来。
采样函数的傅里叶变换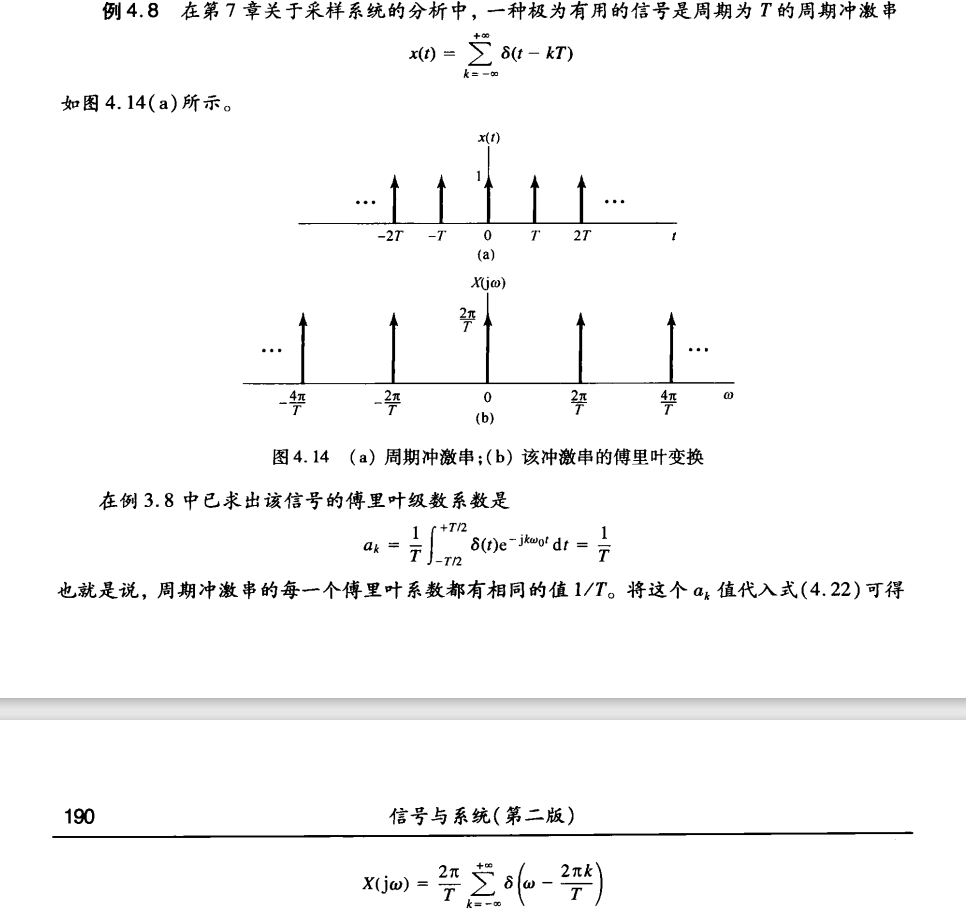

拉普拉斯变换

casual and stable

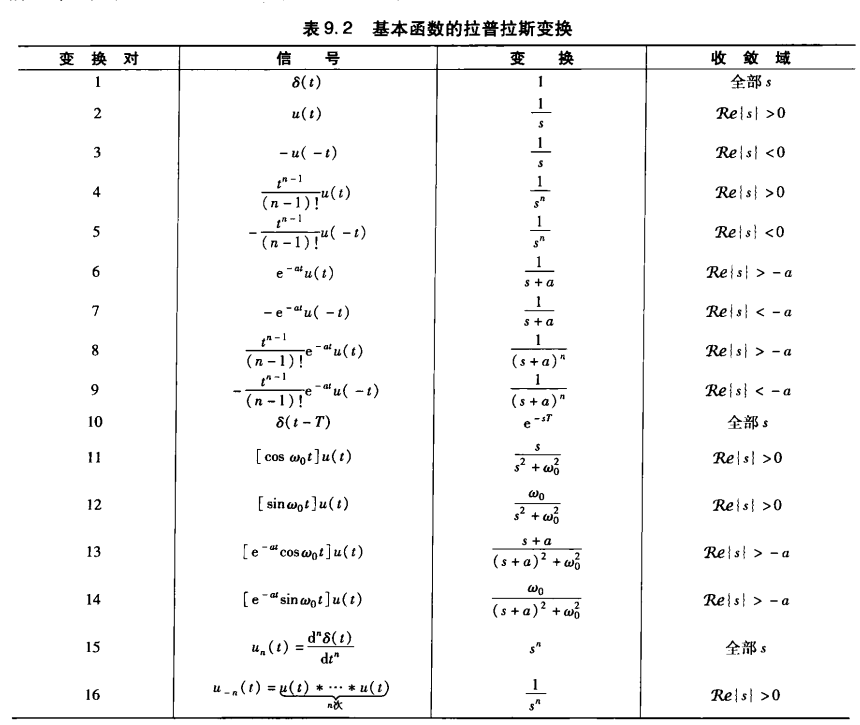
基本函数的拉普拉斯变换

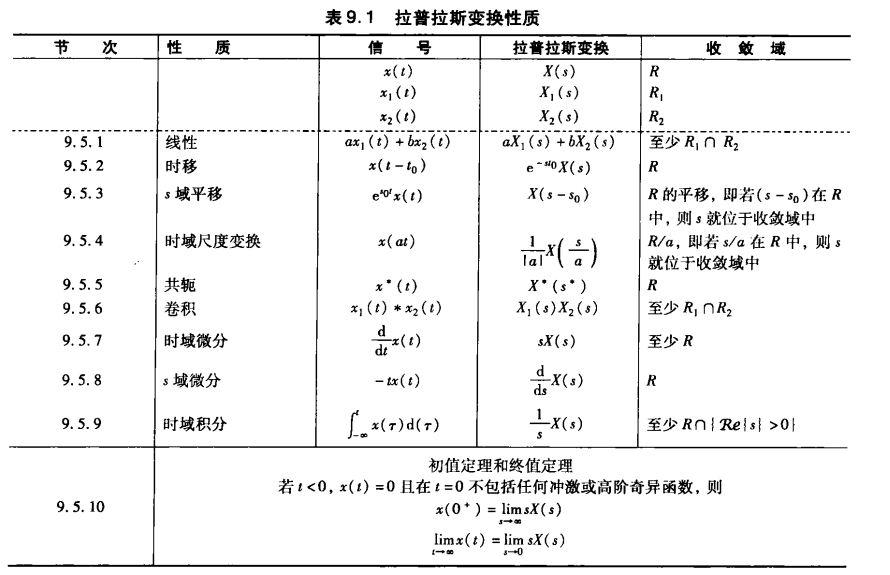
拉普拉斯变换性质

对于一个具有有理系统函数的系统来说，系统的因果性就等效于收敛域位于最右边极点的右边的右半平面。
当且仅当系统函数 H(s)的收敛域包括 j 轴即 Re{s}=0 时一个线性时不变系统就是稳定的

实函数

如果是实函数，那么拉普拉斯变换的零极点共轭对称

输入e的多少t或z的多少n次方