数电

教材链接
常用英文
complement:补码
最高有效位( most significant bit,MSB)指的是一个n位二进制数字中的n-1位,具有最高的权值2^(n-1)。最低有效位和最高有效位是相对应的概念。lsb least significant bit:最低有效位
SM-CODE:符号位
resistive loads:电阻负载
flip-flops:触发器
decimal number:十进制数
binary number:二进制数
octal number:八进制数
hexadecimal number:十六进制数
implicant:蕴含项其实就是卡诺图的“圈”,每一种可能的圈就是一个蕴含项
essential prime implicant:实质本源蕴含项中必须含有至少一个没被包含在其它蕴含项中的项,而且不能被更大的圈包裹
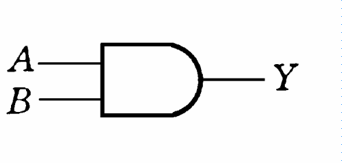
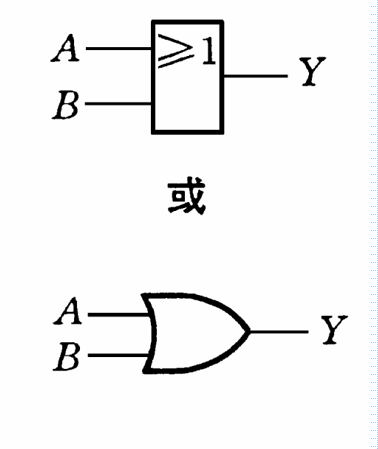
门电路

数制和编码
基数:(base or radix) 计数制中,每一位的基数都是固定的,如十进制的基数是10,二进制的基数是2,八进制的基数是8,十六进制的基数是16。
十进制转化为二进制:
1.整数:除2取余,逆序排列
2.小数:乘2取整,顺序排列
原码:将一个整数转换成二进制形式,就是其原码。例如short a = 6; a 的原码就是0000 0000 0000 0110;更改 a 的值a = -18; 此时 a 的原码就是1000 0000 0001 0010。
通俗的理解,原码就是一个整数本来的二进制形式。
补码表示范围2^(n-1)-1到-2^(n-1)
补码10000000表示-128而在原码中10000000表示-0
128 的二进制原码 10000000,将所有位取反得到 01111111,然后在最低位加 1,得到补码 10000000。这就是 −128的原码。
反码:对于正数,它的反码就是其原码(原码和反码相同);负数的反码是将原码中除符号位以外的所有位(数值位)取反,也就是 0 变成 1,1 变成 0。例如short a = 6; a 的原码和反码都是0000 0000 0000 0110;更改 a 的值a = -18; 此时 a 的反码是1111 1111 1110 1101。
补码:正数的补码是其本身,负数的补码是其反码加1(包括符号位)。
对任意的x,若已知[x]补,则把[x]补连同符号位的每一位都取反再加1即可得到[-x]补。
已知x(x为负数)的补码,求x的原码:将x的补码除符号位外的每一位都取反,再加1,即为x的原码。
加减运算
溢出:
两个操作数具有相同的符号
结果的标志不同
BCD

余3码:十进制数+3
2421码、5211码:0-4最高位为0,5-9最高位为1
格雷码

给定二进制数
- 二进制数的最高位(MSB)与格雷码的最高位(MSB)相同。
- 格雷码的其他位可以通过对二进制数当前位置的位与其下一高位置的位进行异或(XOR)运算来获得。
给定二进制数 ( 0111 ):
- 最高位是 0。
是 1。 是 0。 是 0。
因此,二进制数 ( 0111 ) 的格雷码是 ( 0100 )。
Write the logic expression of a 2-bit adder!
2 input 1 output
Input 2-bit, output 3-bit
一个2位加法器可以用逻辑表达式表示为一个3位输出的逻辑函数,其中输入是两个2位二进制数字(A和B),输出是它们的和(S)和可能的进位(C)。以下是这个2位加法器的逻辑表达式:
对于和(S)的每一位:
S0 = A0 ⊕ B0(个位相加)
S1 = (A1 ⊕ B1) ⊕ (A0 ∧ B0)(十位相加)
对于进位(C)的每一位:
C0 = A0 ∧ B0(个位进位)
C1 = (A1 ∧ B1) ∨ (A0 ∧ B0)(十位进位)
这里的符号表示:
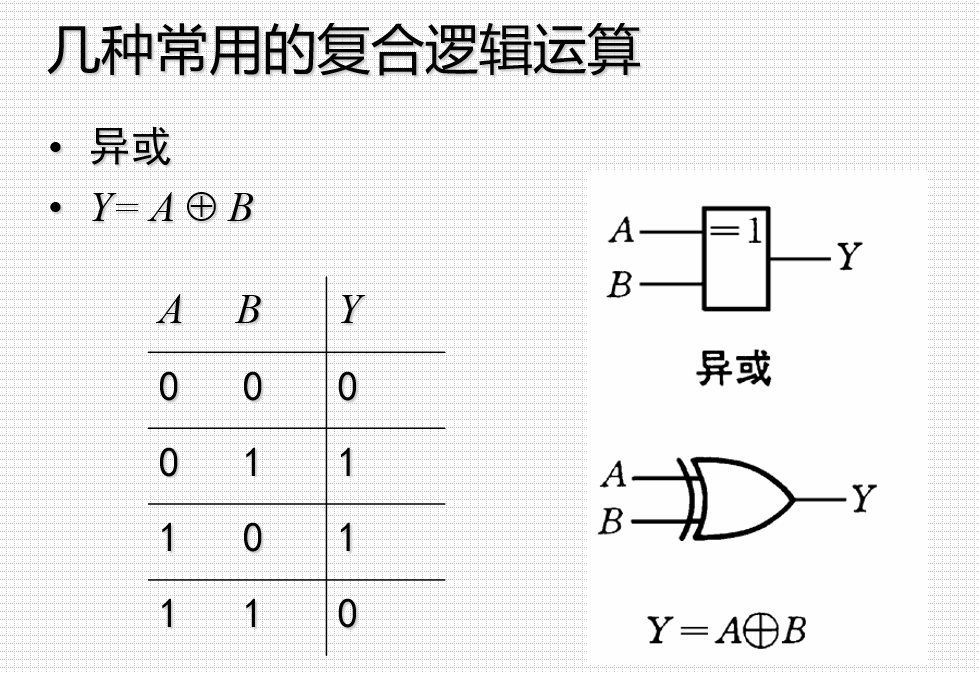
⊕ 表示异或运算,即相同为0,不同为1。
∧ 表示逻辑与运算。
∨ 表示逻辑或运算。
这些逻辑表达式将两个2位二进制数相加,产生一个3位的和和可能的进位。这是一个基本的2位加法器的逻辑表示。
静态冒险
卡诺图有相切的1就有静态1冒险
静态1冒险:在输入变化时,输出出现短暂的0
ADC,DAC
ADC(模数转换器,Analog-to-Digital Converter)和DAC(数模转换器,Digital-to-Analog Converter)是两种用于将模拟信号与数字信号相互转换的关键组件,通常用于数字电子设备中。它们的作用如下:
ADC
ADC(模数转换器):ADC将模拟信号(连续的信号)转换为数字信号(离散的信号)。这通常涉及到将连续的模拟信号在一定时间间隔内进行采样,并将每个采样点的幅度值转换为对应的数字表示,通常是二进制数字。ADC广泛用于数字信号处理、通信系统、传感器数据的读取等应用中。
模数转换器(ADC)是一种将连续的模拟信号(如表示电压的十进制分数)转换为离散的数字表示(二进制分数)的设备或电路。
在将十进制分数转换为二进制分数的情境下,ADC接受模拟输入,通常是表示十进制分数的电压,然后生成对应的二进制表示。
二进制分数通常使用固定位数的比特来表示,其中每个比特表示ADC总范围的特定分数。ADC的精度,通常以数字输出中的比特数表示,决定了二进制分数的粒度,从而影响了从十进制到二进制的转换的准确性。
将模拟输入(十进制分数)转换为二进制分数的过程涉及一系列数学运算,基于数字电子学和二进制算术的原理。得到的二进制分数可以用于进一步的数字处理、存储或传输原始模拟信号。
概念区分
两个反相器能输出高质量信号
分辨率
分辨率(Resolution)是指ADC能够分辨量化的最小信号的能力,用二进制位数表示。
比如:一个10位的ADC,其所能分辨的最小量化电平为参考电平(满量程)的2的10次方分之一。即分辨率越高,就可以将满量程里的电平分出更多份数,得到的结果就越精确,得到的数字信号再用DAC转换回去后就越接近原来输入的模拟值。
所以,对于给定的一个具体ADC器件,其分辨率值是固定的。
精度
精度(Precision)是指对于给定模拟输入,实际数字输出与理论预期数字输出之间的接近度(误差值是多少)。换而言之,转换器的精度决定了数字输出代码中有多少个比特表示有关输入信号的有用信息。
有些ADC器件的datasheet中,会注明精度值或精度范围。
对于给定的一个具体ADC器件,其精度值可能会受外界环境(温度、干扰等)的影响而变化。
区别
分辨率和精度,不要拿在一起混为一谈,其中“精度”是用来描述物理量的准确程度的,而“分辨率”是用来描述刻度划分的。
其实,对于ADC来说,这两样都是是非常重要的参数,往往也决定了芯片价格,显然,我们都清楚同一个系列,16位AD一般比12位AD价格贵,但同样是12位AD,不同厂商间又以什么参数区分性能呢?性能往往决定价格,那么什么参数对价格影响较大呢?此时就要用精度来衡量。
引用一个别人的比喻:有这么一把常见的塑料尺(中学生用的那种),它的量程是10厘米,上面有100个刻度,最小能读出1毫米的有效值。那么我们就说这把尺子的分辨率是1毫米,或者量程的1%;而它的实际精度就不得而知了(算是0.1毫米吧)。
当我们用火来烤一下它,并且把它拉长一段,然后再考察一下它。我们不难发现,它还有有100个刻度,它的“分辨率”还是1毫米,跟原来一样!然而,您还会认为它的精度还是原来的0.1毫米么?
量化间隔:
量化间隔是ADC将模拟信号离散化为数字表示时所采用的最小单位。它表示了ADC能够分辨的最小信号变化。量化间隔的大小由ADC的比特数决定,通常用电压表示。例如,对于一个8位ADC和5V的量程,每个量化间隔的大小为:
量化间隔大小=量程/2^n
其中,n 是ADC的比特数,量程是ADC能够接受的最大电压范围。
精度:
精度表示ADC的输出数字在理论值上与实际模拟输入值之间的最大允许误差。它通常以比特数来衡量,即ADC的输出数字位数。例如,一个8位ADC具有256个离散的输出级别,这意味着它有8位精度。
量化误差:
量化误差是ADC测量的模拟信号与量化后的数字表示之间的差异。它是由量化间隔的大小决定的。量化误差可以被视为量化间隔的一半。对于一个n位ADC,量化误差大小大约为:
量化误差=量化间隔大小/2
这个误差会影响ADC的精度,特别是对于小信号的精度影响较大。
ADC工作原理的理解对于理解模拟信号如何在数字系统中被处理和分析非常重要。ADC是数字信号处理中的基本组件,广泛应用于数据采集、通信、控制系统等领域。
采样速率(Sampling Time)
这里说的采样速率就是我们最高的ADC采样频率,也就是数据手册中的Maximum Sampling Frequency。ADC的采样速率必须小于转换速率,常用单位是 ksps 和 Msps,表示每秒 采样千/百万次(kilo / Million Samples per Second)。
转换时间(Conversion Time)
转换时间的导数就是转换速率。因为将一个模拟信号值转换成一个数字量不能瞬间完成,这个过程需要一定的时间。下图说明了转化时间的基本概念,在t0时刻进行模拟电压值的转换,但是直到t1时刻才完成转换。
量程(full-scale range, FSR)
作为测量元件,量程一定是需要关注的,指的是允许输入的模拟信号范围。
最低有效位(One least significant bit, LSB)
又称最小分辨率,要记住这个参数的英文LSB,满量程值除以ADC的分辨率就是LSB,很好理解,就比如说一个4位的ADC,数字量最高可以表示2的4次方也就是16,满量程5V,那么最小的分辨率就是5/16=0.31V,也就是说这个ADC最小辨认的电压是0.31V,可以用数字量0001表示0.31V这个模拟量。LSB越小表明ADC的精度越高。下图纵坐标是数字量编码,横坐标每一个台阶就代表LSB。
量化误差(Quadratuer Error)
/指由于对模拟信号进行量化而产生的误差,该误差最大可达到量化等级的一半。
例题
Determine the max error of a 8-bit ADC with 5 V scale.
If the analog input is 1.15 V, determine the digital output and its error.A 8-bit DAC’s range is 0-2.5V, if the input is 1010010, calculate its output
对于一个8位ADC,它有256个量化电平(2的8次方),即每个量化间隔为(5 V / 256 ≈ 0.0195 V)。
a. 最大误差:最大误差等于量化间隔的一半,即0.0195 V / 2 = 0.00975 V。
b. 数字输出:对于输入模拟电压1.15 V,其对应的数字输出为 1.15 V / 0.0195 V ≈ 58.97。因为ADC输出是整数,所以四舍五入到最近的整数,即取整后的数字输出为 59。
c. 误差:模拟输入1.15 V对应的量化间隔中点是 1.15 V - 0.00975 V ≈ 1.14025 V。该量化间隔的数字表示是59,对应的电压是59 * 0.0195 V ≈ 1.1495 V。因此,误差是 1.1495 V - 1.15 V ≈ -0.0005 V。
对于一个8位DAC,其范围是0-2.5 V,因此每个量化间隔为(2.5 V / 256 ≈ 0.0098 V)。
a. 给定输入1010010,将其转换为十进制:1010010(二进制)= 82(十进制)。
b. 数字到模拟输出:82(十进制)* 0.0098 V ≈ 0.8036 V。
因此,输入为1010010的8位DAC的输出电压约为0.8036 V。
DAC
DAC(数模转换器):DAC将数字信号转换为模拟信号。它将离散的数字值转换为模拟信号的连续波形。这对于数字音频、视频播放、模拟控制系统等应用非常重要。DAC的输出是一个连续的电压或电流信号,模拟了输入数字信号的变化。
卡诺图
1.卡诺图的圈是可以重复的
2.每个圈中包含的相邻的最小方格数必须是2的整数次幂
3.为了得到尽可能大的圈,圈与圈之间可以重叠
4.若某个圈中标1的方格完全被其他圈所覆盖,则该圈为多余圈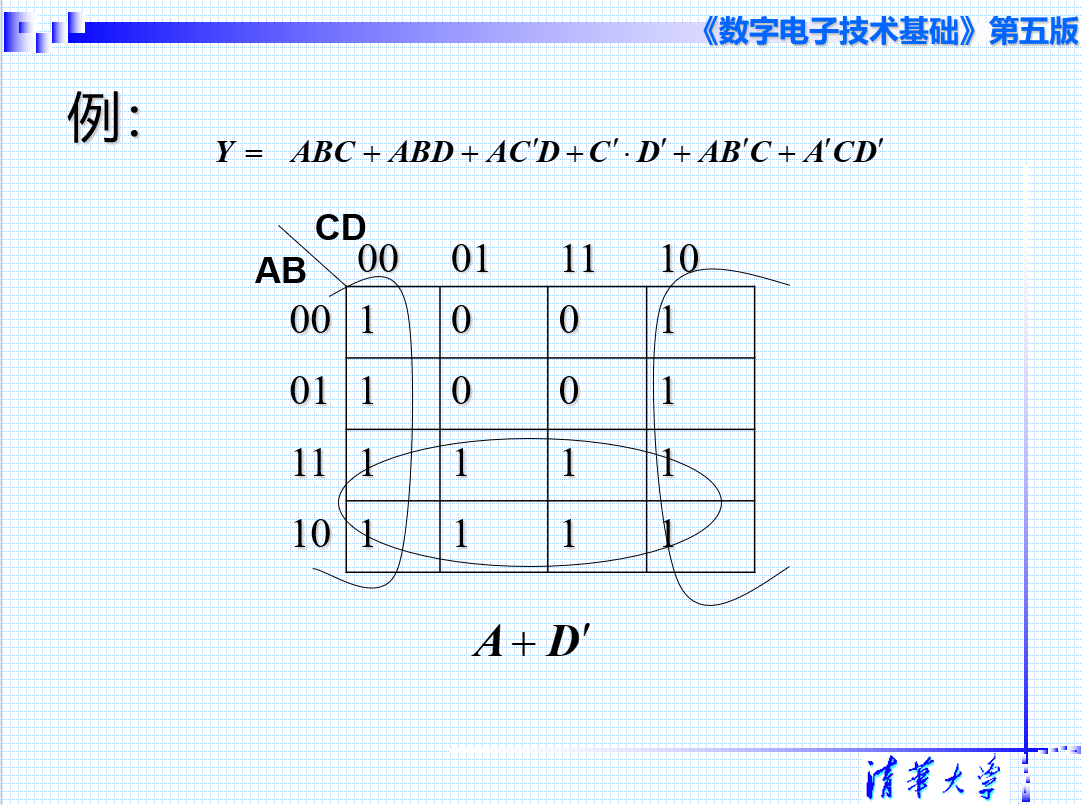
重要公式

最小项最大项转化
mos
半导体载荷
半导体中有两种载流子:自由电子和空穴。电子负电,空穴正电。
不论是P型还是N型半导体,它们本身是不带电的,也就是保持电中性。载流子的浓度不同。
N 型半导体
N 型半导体也称为电子型半导体。N型半导体即自由电子浓度远大于空穴浓度的杂质半导体。(negative)
P 型半导体
P 型半导体也称为空穴型半导体。P型半导体即空穴浓度远大于自由电子浓度的杂质半导体。(positive)
PMOS晶体管工作原理
p型晶体管的工作方式与n型晶体管非常不同当该晶体管接收到非零电压时,它将产生开路,从而阻止电流从栅极 (G) 端子流向源极 (S) 。与此类似,当该晶体管接收到约0伏的电压时,它形成一个闭合电路,这意味着电流从栅极 (G) 端子流向漏极(D)
0输出1,1输出0
n型晶体管反之
NAND门是数字电子电路中的一种基本逻辑门,用于进行逻辑运算。它是由两个输入引脚和一个输出引脚组成。NAND门的输出取决于两个输入的逻辑状态。
逻辑运算规则如下:
当两个输入都为1时,输出为0。
在其他情况下,输出为1。
NOR门(Not OR门)是数字电子电路中的一种基本逻辑门,用于进行逻辑运算。它是由两个输入引脚和一个输出引脚组成。NOR门的输出取决于两个输入的逻辑状态。
逻辑运算规则如下:
当两个输入都为0时,输出为1。
在其他情况下,输出为0。
输入输出都取非,与变或,或变与
##
mealy machine outputs are determined by states and inputs
moore machine outputs are determined by states
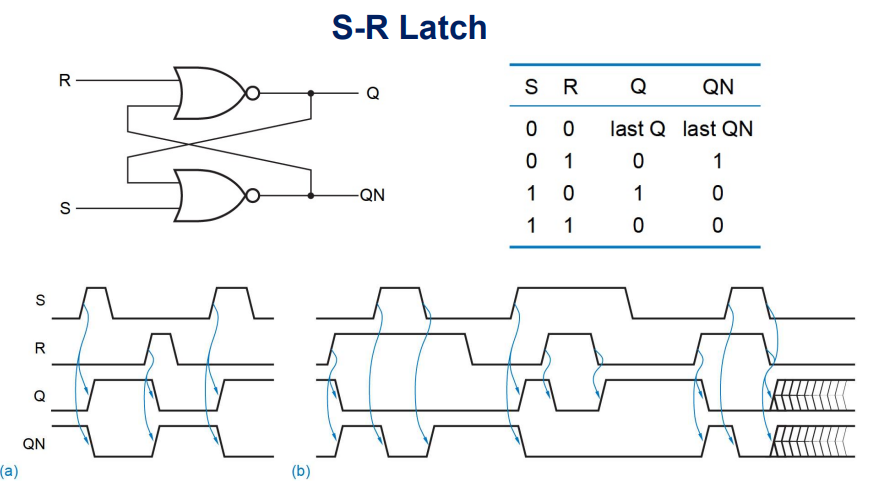
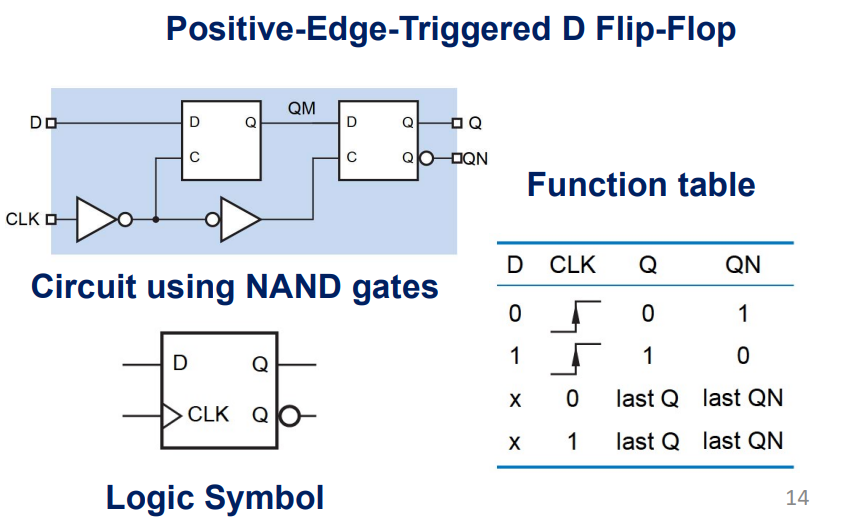
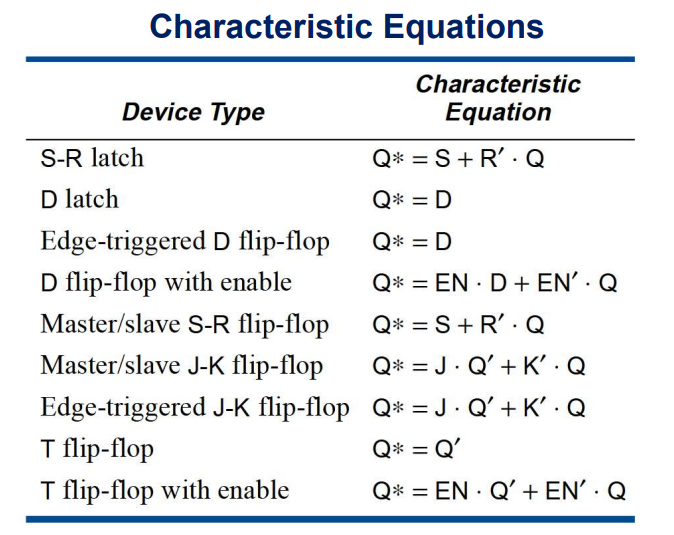
时序电路常用元器件
- Title: 数电
- Author: Ikko
- Created at : 2023-09-13 19:43:33
- Updated at : 2025-12-17 20:43:12
- Link: http://ikko-debug.github.io/2023/09/13/数电/
- License: This work is licensed under CC BY-NC-SA 4.0.
